СВОБОДНЫЙ ПОЛЁТ ЭЛЕКТРОНА
(Систематические ошибки в экспериментах с ускоренными электронами)
Руднев А.Д.
Задача определения скорости свободного полета электрона, получившего предварительное ускорение, является очень важной как
для экспериментальных исследований, так и в теоретическом плане. Например, электронная пушка обеспечивает электрон кинетической
энергией . Какая часть этой энергии сохранится в электроне, если конструктивно до мишени ещё остается некоторое расстояние?
Для ответа на подобные вопросы надо знать законы пространства, определяющего торможение электрона.
Магнитные силы возникают при относительном движении зарядов . Существование магнитных сил в пространстве (в т.ч. - и вакууме)
подтверждает факт структурности пространства свободными электронами [1]. Предварительными исследованиями нам удалось вычислить
плотность свободных электронов в атмосфере Земли 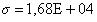
 . И это дает основание надеяться на решение поставленной задачи.
. И это дает основание надеяться на решение поставленной задачи.
Рассматривая движение электрона в среде пространственных электрических зарядов (ПЭЗ), необходимо найти степень жесткости структуры.
В качестве такого параметра предлагается принять производную от кулоновской силы по расстоянию
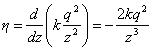 (1)
(1)
где 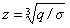 - сторона условного куба структурной решетки.
- сторона условного куба структурной решетки.
С подстановкой [1]
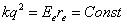 (2)
(2)
получаем жесткость пространства в функции энергии свободных электронов
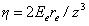 (3)
(3)
Численное значение этого параметра 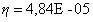
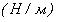 говорит об относительной податливости среды, об её способности уступать малейшим
внешним воздействиям. Однако, мы знаем, что такая податливость вызывает дополнительные взаимодействия
электронов между собой. При этом интегральный импульс взаимодействия
говорит об относительной податливости среды, об её способности уступать малейшим
внешним воздействиям. Однако, мы знаем, что такая податливость вызывает дополнительные взаимодействия
электронов между собой. При этом интегральный импульс взаимодействия
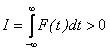 (4)
(4)
рождает силу магнитного торможения при произвольном характере движения.
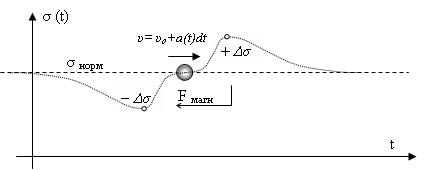
Следовательно, любое движение электронов можно представить как сумму равномерного и ускоренного движений, причем обе составляющие скорости будут
получать магнитное торможение, хотя и различное. Впереди движущегося электрона будет создаваться уплотнение ПЭЗ, а позади него- разрежение. Тогда
компонента ускоренного движения отвечает за объем уплотнения, а компонента равномерного движения - за поддержание сформированного барьера (рис.1).
Рис.1. Формирование волны давления движущимся зарядом.
Если, любой вид движения состоит из элементарных актов взаимодействий с отдельными электронами среды, получается, что перемещение пробного
электрона на некоторое фиксированное расстояние требует преодоления одинакового числа 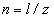 актов (4) независимо от характера скорости.
Только интенсивность этих актов взаимодействия различна. Интенсивность актов зависит от давления магнитных сил ПЭЗ
актов (4) независимо от характера скорости.
Только интенсивность этих актов взаимодействия различна. Интенсивность актов зависит от давления магнитных сил ПЭЗ
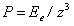 (5)
(5)
а точнее- от высоты барьера 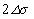 . Известно, что магнитное давление динамическое и создается колебаниями ЭМ свободных электронов [2]. Скорость волн давления равна световой,
а это значит, что барьер образуется за счет разности скоростей
. Известно, что магнитное давление динамическое и создается колебаниями ЭМ свободных электронов [2]. Скорость волн давления равна световой,
а это значит, что барьер образуется за счет разности скоростей 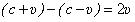 . Отношение
. Отношение 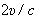 масштабирует действующее на электрон давление.
В таком случае сила торможения движущегося электрона равна
масштабирует действующее на электрон давление.
В таком случае сила торможения движущегося электрона равна
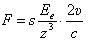 (6),
(6),
где 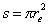 - площадь сечения электрона.
- площадь сечения электрона.
Деформация ПЭЗ равна отношению
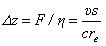 (7),
(7),
а энергия деформации , определяющая потери на удержание созданного барьера, равна
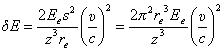 (8),
(8),
Электрон теряет энергию на удержание барьера. Поскольку полная энергия электрона равна 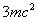 ,
то энергия поля электрона уменьшается в k раз
,
то энергия поля электрона уменьшается в k раз
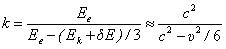 (9),
(9),
Возвращаясь вновь к силе (6), находим отрицательное ускорение, тормозящее свободный полёт электрона
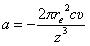 (10),
(10),
На рис.2 показан расчетный график торможения электрона без столкновений с атомами или молекулами с начального значения скорости 0,001C.
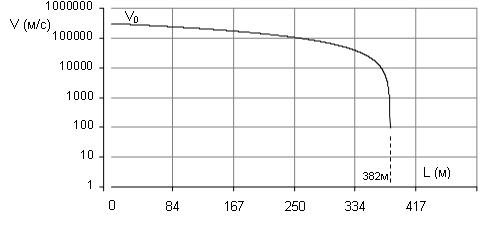 Рис.2. Спад скорости движения электрона в среде ПЭЗ.
Рис.2. Спад скорости движения электрона в среде ПЭЗ.
Такой электрон должен пролететь 382м и на скорости 93 м/с остановится, как захваченный структурой ПЭЗ.
Из данного материала следует, что современная физика допускает значительную погрешность вычислений кинетической энергии ускоренных электронов, не учитывая торможения ПЭЗ.
Ускорение торможения эквивалентно действию обратной электрической напряженности ~ 2,67 В/м (при v=c). Прямое ускорение электронов электрическим полем можно представить упрощенно,
вычислив в формуле (10) постоянные члены
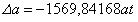 (м/с^2) (11),
(м/с^2) (11),
Сравнительные графики для скорости электрона при напряженности поля 5(В/м) приведены на рис.3.
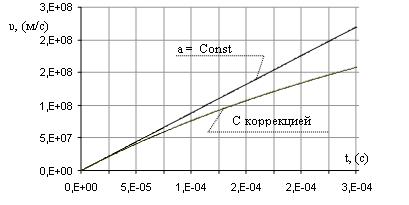 Рис.3. Графики скорости электрона с учетом магнитного торможения и без него.
Рис.3. Графики скорости электрона с учетом магнитного торможения и без него.
Мы видим, что погрешность достигает 30%, а расчетная энергия окажется на порядок выше.
Кроме того, при поступательном движении электрона расходуется только энергия меридионалных колебаний энергомассы, создающих магнитное поле электрона.
Орбитальная энергия вращения, создающая потенциал, неизменна. Именно по этой причине статическое поле электрона деформируется в движении, становится сферически несимметричным. А это значит,
что орбитальный радиус электрона и электрический потенциал поля (и масса -тоже) сохраняют свои значения.
И -как следствие,- отношение энергии к потенциалу уменьшается.
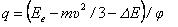 (12),
(12),
Погрешности растут также и в определении числа электронов в пучке. Происходит то, о чем я давно твержу: заряд электрона
не является фундаментальной константой, его значение падает с ростом скорости электрона. Именно это обстоятельство проявляется во взаимодействии летящих электронов в ускорителях.
А потом начинается процесс "разгадки" причин [3] расхождения теории и практики. Разумеется, с введением ложных предположений
ССЫЛКИ:
1. Руднев А.Д. Шаг к структуре пространства. http://www.sciteclibrary.ru/rus/catalog/pages/8182.html
2. Руднев А.Д. Новая концепция физики . http://www.sciteclibrary.ru/rus/catalog/pages/6910.html
3. В. Петров. Движение электронов в однородном электрическом поле линейного ускорителя.
http://bourabai.narod.ru/petrov/el_motion.htm
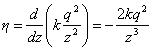 (1)
(1)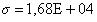
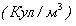 . И это дает основание надеяться на решение поставленной задачи.
. И это дает основание надеяться на решение поставленной задачи.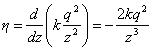 (1)
(1)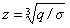 - сторона условного куба структурной решетки.
- сторона условного куба структурной решетки.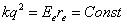 (2)
(2)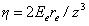 (3)
(3)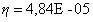
 говорит об относительной податливости среды, об её способности уступать малейшим
внешним воздействиям. Однако, мы знаем, что такая податливость вызывает дополнительные взаимодействия
электронов между собой. При этом интегральный импульс взаимодействия
говорит об относительной податливости среды, об её способности уступать малейшим
внешним воздействиям. Однако, мы знаем, что такая податливость вызывает дополнительные взаимодействия
электронов между собой. При этом интегральный импульс взаимодействия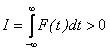 (4)
(4)
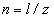 актов (4) независимо от характера скорости.
Только интенсивность этих актов взаимодействия различна. Интенсивность актов зависит от давления магнитных сил ПЭЗ
актов (4) независимо от характера скорости.
Только интенсивность этих актов взаимодействия различна. Интенсивность актов зависит от давления магнитных сил ПЭЗ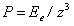 (5)
(5)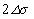 . Известно, что магнитное давление динамическое и создается колебаниями ЭМ свободных электронов [2]. Скорость волн давления равна световой,
а это значит, что барьер образуется за счет разности скоростей
. Известно, что магнитное давление динамическое и создается колебаниями ЭМ свободных электронов [2]. Скорость волн давления равна световой,
а это значит, что барьер образуется за счет разности скоростей 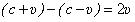 . Отношение
. Отношение 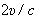 масштабирует действующее на электрон давление.
В таком случае сила торможения движущегося электрона равна
масштабирует действующее на электрон давление.
В таком случае сила торможения движущегося электрона равна
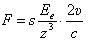 (6),
(6),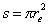 - площадь сечения электрона.
- площадь сечения электрона.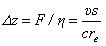 (7),
(7),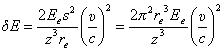 (8),
(8),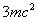 ,
то энергия поля электрона уменьшается в k раз
,
то энергия поля электрона уменьшается в k раз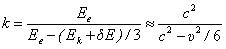 (9),
(9),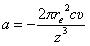 (10),
(10),
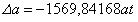 (м/с^2) (11),
(м/с^2) (11),
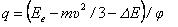 (12),
(12),