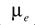, к его механическому моменту,
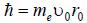, равно
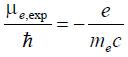(1)Этот результат превысил ожидаемое (следующее из теории) значение, равное
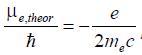(2),в два раза (знак минус указывает, что направление моментов противоположны).
Совершенно очевидно в данной ситуации было бы разумным тщательно проверить правомерность использования соответствующих элементарных формул, используемых при теоретическом выводе величины
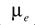. По определению, которого современная физика придерживается и до сих пор, расчет орбитального магнитного момента электрона в атоме осуществляется по простой формуле, определяющей магнитный момент замкнутого электрического контура,
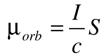(3),где I - средняя величина кругового тока, S - площадь орбиты, c - скорость света.
Следуя механической модели определения тока, используемой в электротехнике, как потока электрического заряда ("электронной жидкости") в проводнике, вычисление средней величины силы электрического тока, создаваемого вращающемся электроном, осуществлялось (как выясняется здесь, непродуманно и ошибочно) по формуле
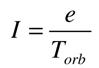(4),где Т орб - период обращения электрона имеющего заряд е по орбите. Отсюда,
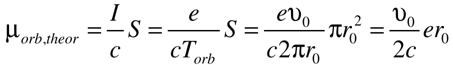(5),что привело к отношению моментов (2), в 2 раза отличающегося (меньшего) от полученного экспериментально значения (1). Нужно было искать ошибку.
Никто тогда почему-то не задался вопросом, а правомерна ли формула (4); она прежде всего должна была привлечь внимание теоретиков. Ведь мы имеем дело не с силой тока "электронной жидкости" (или "электронного газа"), а с силой тока генерируемого одиночным зарядом, причем, движущимся по замкнутому контуру, кругу. Исправим их ошибку.
1. Рассмотрим какую же в действительности среднюю величину тока создает одиночный (дискретный) заряд, движущийся по замкнутой траектории.
В общем случае перенос заряда е элементарной частицей, электроном, через любое сечение S по любой траектории за время Т сопровождается его исчезновением с одной стороны (-е, точка А) произвольного сечения и появлением на другой стороне (+e, точка В), как показано на рисунке.
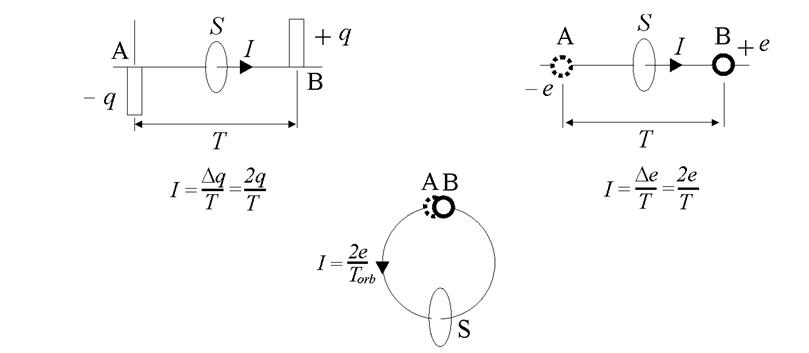
Отсюда, средняя скорость изменения заряда (ток I) за время Т равна
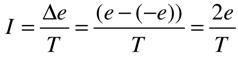(6),А в случае круговой орбиты, когда точки А и В совпадают, электрон, обладающий зарядом е, проходит через поперечное сечение S со средней скоростью
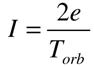(7),где Т орб -есть период обращения электрона по круговой орбите.
2. Поскольку электрон, как и любая другая элементарная частица, проявляет двойственность поведения, и как частицы и как волны, без всякого сомнения представляется целесообразным и необходимым выведение формулы средней величины тока и для случая волнового движения электрона.
а) Начнем с одномерной задачи. Из хорошо известного решение волнового уравнения для струны длиной l, фиксириванной с обоих концов, следует, что только одна полуволна фундаментального тона помещается на полной ее длине,
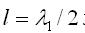. Если соединить концы струны вместе, то образуется круг длиной 
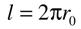с одним узлом. В результате получим равенство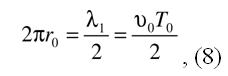
где Т0 -есть волновой период,
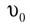- волновая скорость в струне.б) В простейшем трехмерном случае решения волнового уравнения для сферического поля [1] мы приходим к тому же равенству (8): только одна полуволна фундаментального тона помещается на Боровской орбите, и электрон находится в узле волны. Таким образом (см. (8)), величина волнового периода фундаментального тона на волновой поверхности радиуса r0 равна
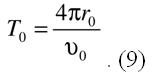
Средняя величина тока, как гармонической величины, определяется по известным формулам:
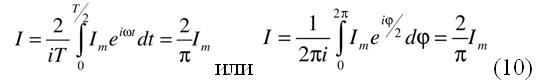
Амплитуда элементарного тока Im , входящая в выражение (10), равна
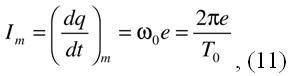
где
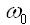есть частота фундаменального тона электронной орбиты. Таким образом, подставляя (11) в (10), получаем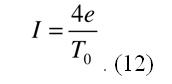
Или, поскольку
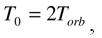
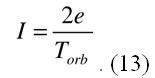
Задача решена, ошибка найдена. Полученная формула для силы тока отличается от используемой теоретиками формулы (4), при рассмотрении ими указанного выше эксперимента, наличием множителя 2. В работе [1] приведены также другие варианты вывода средней величины тока для электрона, движущегося по круговой орбите. Все они дают одну и ту же величину, определяемую формулой (13), а не формулой (4). Подставляя среднюю величину тока (13) в формулу (3) находим правильную (логически, физически и математически обусловленную) формулу для вычисления орбитального магнитного момента электрона, которая ни у кого уже не может вызывать сомнения,
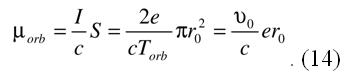
Отсюда, отношение орбитального магнитного момента электрона (14) к его механическому моменту (моменту его орбитального импульса,
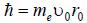), с учетом знака (противоположной направленности моментов), равно
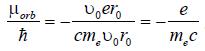(15)Полученное отношение моментов, теоретический вывод которого представлен выше, совпадает с отношением моментов (гиромагнитным отношением) (1), полученным экспериментально в опытах Эйнштейна и де Хааса и в опытах Барнетта.
ЗАКЛЮЧЕНИЕ
Истинная величина собственного магнитного момента электрона, связанного в атоме, пренебрежительно мала по сравнению с приписанным ему значением в половину орбитального магнитного момента (равного магнетону Бора). Какова его конкретная величина и как она была вычислена можно найти в работе [2]. Надеюсь нами достаточно понятно и убедительно показано, что если на 100% доверять экспериментальным результатам, то, действительно, теоретикам следовало бы прежде всего поискать явную ошибку в формуле, используемой ими при вычисления электрического тока, создаваемого дискретным одиночным зарядом (электроном), движущимся по орбите, а не заниматься вымыслом. Сила тока I это единственная физическая величина, от которой зависит магнитный момент, при постоянных c и S (см. формулу (3)). При математической формулировке существующего в физике определения силы тока для такого специфического случая, каким является движение одиночного заряда по замкнутой траектории, нужно было быть внимательным и думать (ведь не зря бытует поговорка: "семь раз отмерь, один раз отрежь"). Это элементарная задача, она по силам и школьникам и студентам, хороша для развития их мышления. Кажется просто, "как грабли", но почему-то эта задача не была решена теоретиками, по-видимому, просто не рассматривалась ими. К сожалению, в результате такой их явной, мягко говоря, недоработки физика пошла по ложному пути. Чтобы выйти из положения, в котором оказались со своим результатом (2), физики-теоретики предпочли пойти по проторенному их предшественниками пути и ввели постулат о собственном механическом моменте электрона, названном ими спином. А именно, чтобы найти недостающую в расчетах половинку в отношении (2), для подгонки к эксперименту, они приписали электрону, обладающему реальными (неотъемлемыми) свойствами, такими как масса и заряд, дополнительно к ним виртуальное, мифическое, а потому нереальное свойство, спин. Как следствие этого, появился соответствующий мифическому спину и мифический собственный (спиновый) магнитный момент электрона, абсолютная величина которого была названа магнетоном Бора,
:
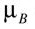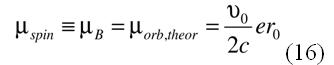
С помощью мифического спинового магнитного момента теоретики "закрыли брешь" в своих расчетах гиромагнитного отношения (2). Таким образом, "утерянную" при расчетах половинку орбитального магнитного момента электрона, связанного в атоме, теоретики назвали спиновым магнитным моментом электрона. Затем эту "утерянную" орбитальную половинку (уже под новым названием, спиновым магнитным моментом или магнетном Бора) прицепили к полученной ими теоретически половинке орбитального магнитного момента (5):
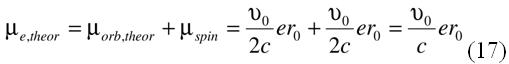
Сложенные вместе две половинки, как видим, по существу одного и того же орбитального магнитного момента, были названы полным магнитным моментом электрона в атоме,
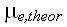. Путем такой явной и элементарной подгонки получилось нужное для совпадения с экспериментом (1) гиромагнитное отношение:
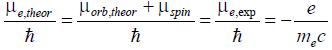(18)Это была эпохальная ошибка, она положила начало настоящей спиномании в физике, продолжающейся до сих пор. Современная физика уже не может существовать без спина. Кому-то, по-видимому, очень нужно было отбросить человечество в его познании природы на столетие назад, направив физику по ложному пути создания виртуальной действительности: загоняя физику в тупик, затормозить развитие нашей цивилизации. Осознанно или нет, но в подобного рода абсурдных (виртуальных) творениях 20-го столетия приняли участие многие выдающиеся физики-теоретики того времени ... Существует мнение, что наличие собственного механического момента, спина, у электрона (а спину приписана сравнительно огромная величина,
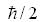, как и орбитальному механическому моменту) подтверждено экспериментально. Однако, где прямые доказательства? Где эксперименты по опредлению величины спина на свободных, а не связанных с атомами электронах? Их нет.Таким образом, объясняя ряд явлений, обнаруженных экспериментально, физики, используя мифические (выдуманные, постулируемые) понятия, подобные спину электрона, рассмотренного здесь, или подобно виртуальным частицам квантовой электродинамики (которые будут рассмотрены далее) рисуют искаженную картину действительности, по сути, создают виртуальный, мифический мир (science fiction).
ЛИТЕРАТУРА
[1] G. P. Shpenkov and L. G. Kreidik, On Electron Spin of , HADRONIC JOURNAL, Vol. 25, No. 5, 573-586, (2002).
[2] G. P. Shpenkov, Theoretical Basis and Proofs of the Existence of Atom Background Radiation, Infinite Energy, Vol. 12, Issue 68, 22-33, (2006);
23.04.2011
Материалы с сайта
Шпенькова Г.П.
Назад
На главную
